We study the Ponzi scheme and different variables’ impacts, such as withdrawal rates, user growth rates, ceiling and so on.
Impacts of Different Variables
With reference to the basic model constructed in Part 1:
We have just assumed that there are two main purposes for Ponzi projects:
- Extend the life cycle of the scheme;
- Have a higher balance.
Next, let’s take a look at the impacts of different variables on these two factors.
Impact of Withdrawal Rate
Suppose that other conditions remain unchanged, set the withdrawal rate from 1% to 99% respectively to calculate the life cycle and balance of the scheme.


We can deduce from the chart that for a scheme project, minimizing user’s withdrawal rate can significantly alleviate its cash flow pressure, extend the life cycle and gain maximum profits.
Impact of Rate of Return, User Growth Rate, and Sales Cost
Higher rate of return (RoR) means an exponential increase of interest the project needs to pay back.
However, the Ponzi scheme is a game of “borrowing from newcomers to pay old users”.
No matter how high the promised RoR is, fraudsters can always fulfil it as long as the growth rate of new users keeps up. In most cases, a higher RoR is more attractive to users. But it is worth noting that when frequent financial scandals are exposed in traditional markets, and the RoR of a project exceeds a certain threshold, it may adversely raise suspicion, leading to the decline in the user growth rate.

In our initial hypothesis, if there is no cap on the number of users, such model can run constantly simply by setting the user growth rate of each round at 10% as shown in the following figure.

If there is no limit to user growth rate, then in calculating the number of participants in an exponential function, we can see that even there are only 100 participants at the initial stage; growing at a rate of 10% after 166 months, the total participants can exceed 7 billion.

This is obviously impossible.
Surely, in the real world, when the number of participants reaches a certain scale, it will inevitably be constrained by factors such as geography, population, and culture, cutting off the sustainable growth of users. See, a ceiling exists.
Impact of Ceiling
Still, assume that there are 100 initial participants but increase the growth rate to 30% per period. When the number of newcomers reaches 20,000 in a certain period, the growth rate will stagnate and start to decline by 5% per month until it reaches zero.
Let’s take a look at the changes in cash flow ceteris paribus.

When the user growth reaches a ceiling and starts to decline, the growth of net inflows drops sharply right the next month, and the balance soon turns to zero.
So, a ceiling can greatly restrict the scaling of the Ponzi scheme.
To study further, we can see that the withdrawal rate and rate of return have little effect on the life cycle when users grow at a high rate. Yet, once the participants reach a ceiling, the lower withdrawal rate can buy more time for the scheme.
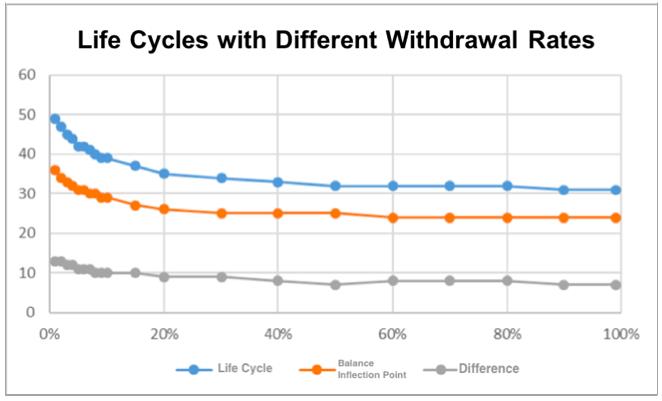
Similarly, toggle the withdrawal rate from 1% to 100% and look at the life cycle and balance inflection point (from which the project will begin to make ends meet by using the former balances to cover interest). We find that after the withdrawal rate is decreased to 20%, both life cycle and the difference of balance inflection points are increased from 9 months to 13 months.
When a Ponzi scheme reaches the balance inflection point, a lower withdrawal rate can help buy more time for the project.

Case Study: Ezubao
Ezubao, a peer-to-peer lender, is founded in February 2014 and based in China’s Anhui province.

Ceiling
In 2015, the estimated turnover of nationwide P2P platforms was less than 1000 billion with an average monthly turnover at 100 billion. Assuming that its users can expand nationwide without geographic restrictions, and eventually occupy 10% of market share; it can gain a maximum monthly income of 10 billion RMB.
Cash Outflow
The average annualized rate of turn of Ezubao is 12% with a monthly RoR of 1%; the monthly commission is calculated at an average of 0.5%; and assume conservatively that there are miscellaneous costs accounting for 20% of monthly total income (i.e. labor costs, workspace rental, registration fee of multiple shell companies, posting pictures of luxury cars pretending to be rich to attract new investors, as well as internal speculation).
Therefore, its monthly cash inflow needs to grow steadily at a rate of 21.5% or more to survive. (Ps. the turnover amount here includes the re-investment amount.)
Judging from this, when the monthly turnover exceeds 10 billion or the monthly growth rate is lower than 21.5%, it is highly possible that the Ezubao scheme will collapse.

Looking from the actual data, Ezubao’s turnover in September 2015 already exceeded 10 billion (reached 13.45 billion). Turnover was 16.211 billion and 16.232 billion for October and November, growing by 20.5% and 0.1% respectively. The probability of Ezubao going bankrupt has increased greatly since October and the actual “detonation” time was right on December 3, 2015.
Though such a model is just an estimate, it is possible to predicate when a Ponzi scheme will collapse by estimating the ceiling and monthly cost.


Please contact me sir, 314-322-7491
Or email me