We humans love to hear and tell stories. We are destined to naturally look for patterns in our day to day life events and we like to connect the dots, relate one event to another (correlate), to tell a compelling story that is strongly persuasive and cohesive, about what we think is happening, which in some cases could be drastically different to what is actually happening. Each individual has a distinct and a unique perception and reflection towards the world.
So, the Correlation:
Correlation in general terms is set to imply a relationship, a connection or an association between two things or two events. In statistics, correlation generally implies the measure of how related the two things or events are, it essentially measures the degree of the relationship between the two.
Statisticians and analysts use a measure called the correlation coefficient, to measure the strength of the relationship between two relative things. There are a number of types of correlation coefficients and the most commonly used one and an easily interpretable one is the Pearson correlation coefficient. It measures the strength based on the well-known and every one’s favourite ‘linear relationship’ between the two variables in consideration.
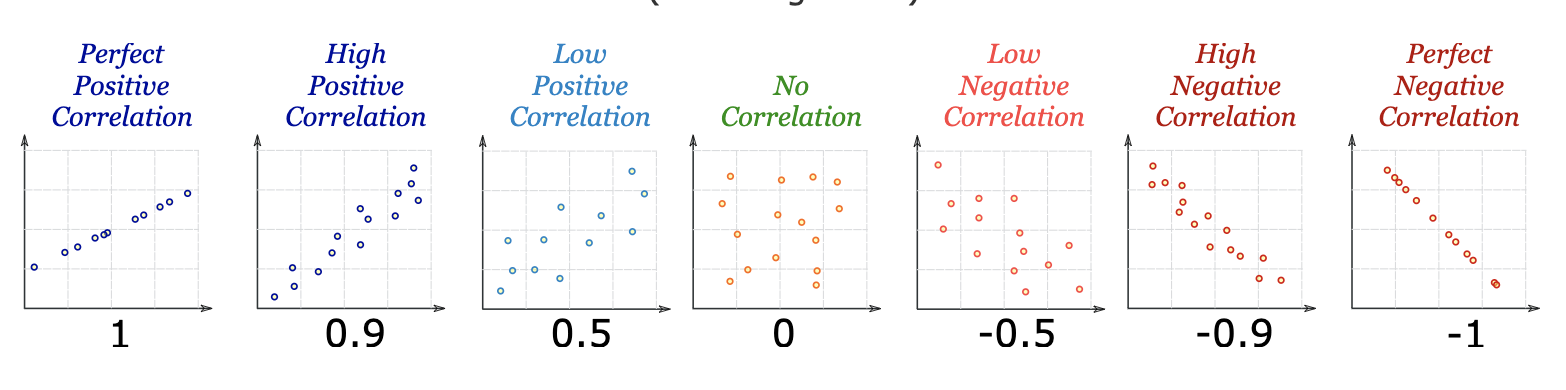
We will call the two events/things to be A and B. So this number describes the relative change in A, with respect to the change in B. The positive values of the correlation coefficient indicates that the value of A increases with the increase in the value of B. On the same lines, a negative correlation coefficient means that, say, the value of A increases with the decrease in the value of B. The values of 1 and -1 indicate a perfect positive and a perfect negative correlation. The value of 0, indicates that there is no linear relationship between the two, and that we cannot establish a relation between the two, by considering the increase or decrease in their values.
The correlation statistics and their visual representations (the scatterplots) are widely used in many practical applications, not only by analysts or statisticians, but by everyone to identify trends, to predict the value of one based on the other, to tell compelling narratives and sometimes even to draw conclusions. The significance of the correlation coefficient values is highly contextual, based on who is carrying out the analysis and for what purpose
So the Causation:
Another concept that is tightly coupled with correlation is the causation. Causation means that one event has caused another, or that one event happens as the result of the other event. This indicates that there is a causal relationship between the two events, event A being the cause and event B being the effect of event A or vice versa.
Correlation Vs Causation:
“Correlation is not causation” is a popular and a more commonly overlooked mantra in statistics.
Sometimes, when using the correlations to draw conclusions, a simple association between two factors can lead to the assumption that one factor/event caused the other. But in reality, the fact is that just because there exists an association between two events, is does not necessarily mean that one of them is the cause of the other.
But often times, it is easily overlooked, when the correlation seems to be in line with a well-known or a popularly believed prejudice or when the correlation appeals to make a lot of sense or when the such an assumption helps in making a compelling story/headline.
A popular misconception that leads to this assumption is called the post hoc fallacy. Fallacies are errors in reasoning and post hoc fallacy is the conclusion that event A is the cause of event B, just because event B followed event A.
The correlation that we see between any two factors/events/things could be
1. Purely produced by chance, that is if the correlation experiment is repeated again with a different set of values for the same two events, it could produce totally a different result.
In the below example, you could see that the mozzarella cheese consumption is positively correlated with the Civil engineering doctorates awarded. The correlation is close to 96%, while these are apparently two very very unrelated events, meaning that there can never be a causal relationship between the two. These kind of spurious correlations are widely present.
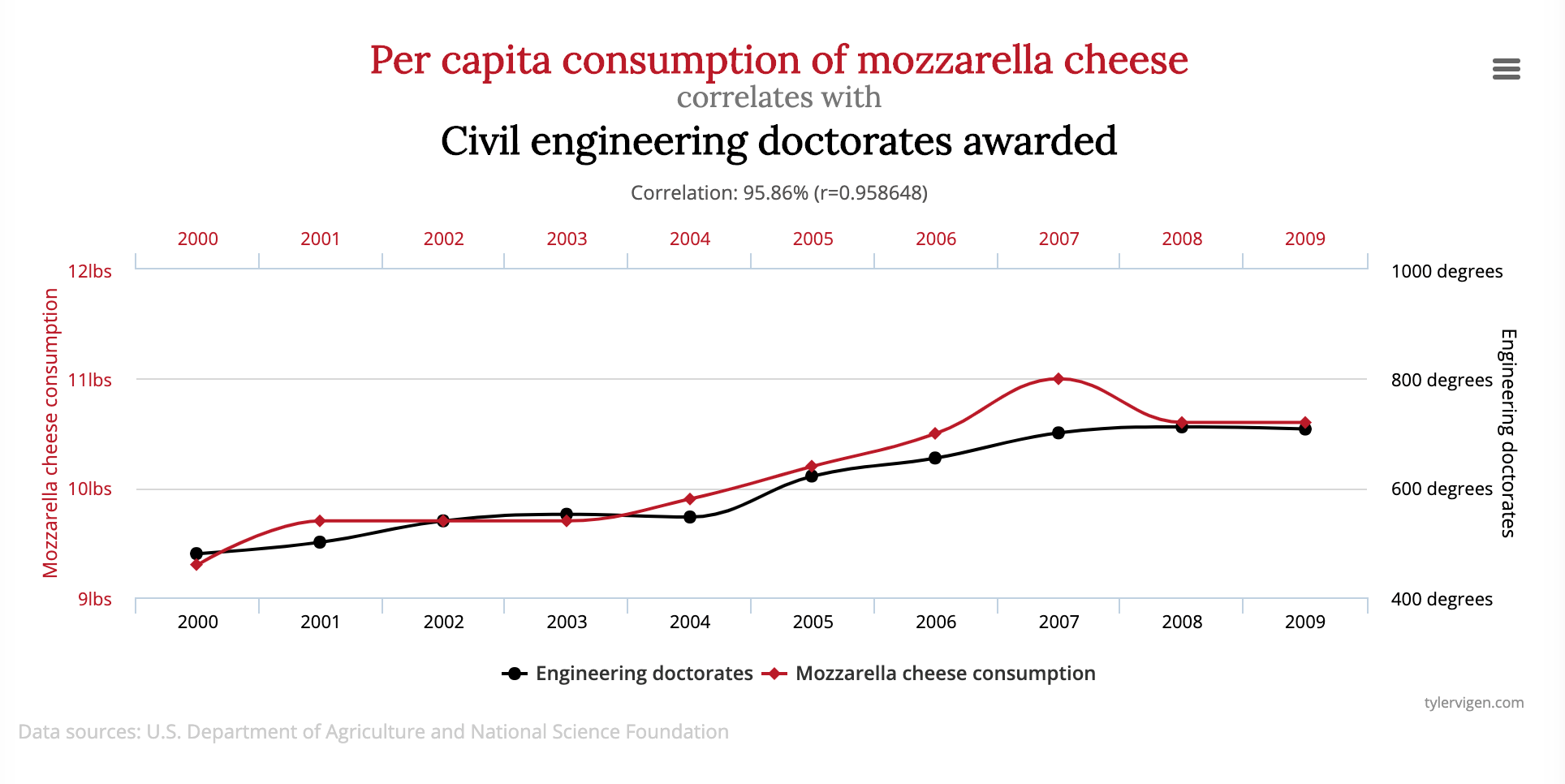
2. The correlation could be real, meaning that it is not produced by a mere chance, and the two events are actually correlated, but it is not obvious that which one of them is the cause and which one is the effect. It could also happen that, the cause event and the effect event might switch places from time to time.

A classic example of this scenario is the correlation between stocks owned by a person and the income of that person. The more money the individual makes, the more stock he/she buys. In this case, earning more income seems to cause the buying of stocks. As the person who invests in stocks also earns from that investment, it is possible that the more stock an individual buys, the more money he/she makes. So in this view, buying of more stocks seems to have caused more income. It is obviously not so accurate to conclude that one event has caused the other.
3. The correlation between the two are real, but in this case there is a third event/factor which influences both the events. This third factor is referred to as the confounding factor.

A simple example of this would be the correlation between alcohol consumption and mortality rate. To study this correlation, often the researchers compare the relationship of alcohol consumption between the people who consume alcohol and the people who do not consume alcohol. It is natural and intuitive to assume that increase in alcohol consumption causes increase in mortality rate. But, actually there could be other factors, like age, healthy eating habits, daily activity levels, that have an effect on the mortality rate. These other factors are the confounding factors.
In some cases, ignoring the effect of a confounding factor and assuming a blind causal relationship between the two events, could lead to conclusions that are not really appropriate and do not reflect the actual scenario at all.
Keep a close eye on these statistical figures :
It is easy to choose a conveniently small sample, to establish a substantial correlation between two events/factors of interest. We witness this kind of statistical figures suggesting correlations every day. It is important to remember that the correlation analysis can only uncover associations and that they cannot determine which one of the events is the cause and which one is the effect. It is also important to note that the correlation statistics do not come alone, just as a fancy number, but in many cases they also bring along a fancy and a totally unwarranted conclusion with them.
With the help of technological advancements, firms across industries are collecting more and more data, with the aim to gather useful insights in order for them to make the right observations, to make the right conclusions and eventually to make the right decisions. It is increasingly important to watch out for these unwarranted conclusions, based on correlations as it could cause potential damages in real-world applications where huge finances and many other things are at stake.
References :
- Inspired by the book – ‘How to Lie with Statistics’ by Darrell Huff
- https://www.theguardian.com/science/blog/2012/jan/06/correlation-causation
- https://www.students4bestevidence.net/blog/2018/10/01/a-beginners-guide-to-confounding/
- Picture Source : Google

